Der Zufall ist eine zwiespältige Sache. Auf der einen Seite wird er gemieden wo es nur geht. Manchmal wird der Vermutung, etwas sei nur per Zufall so passiert, heftig widersprochen, zum Beispiel weil dadurch die eigene Leistung geschmälert würde. So sieht es auch ein bekannter Fußball-Trainer:
Eine schöne Kombination auf dem Fußballplatz ergibt sich
nicht einfach so. Schönheit ist die Abwesenheit von Zufällen.
(Felix Magath, in "Brand Eins", Heft 2, März 2004, S. 75)
Auf der anderen Seite wird der Zufall bei vielfältigen Anwendungen gebraucht und genutzt. Hier lassen sich Verschlüsselungsverfahren, wissenschaftliche und wirtschaftliche Simulationen sowie Spiele anführen. Aber dabei ist es oftmals auch erwünscht den Zufall nachbilden und wiederholen zu können, zum Beispiel um ein Experiment oder eine Simulation zu überprüfen.
Können Sie Zufall erkennen?
Überall kann (vermeintlicher) Zufall besichtigt werden: das Muster der Wolken am Himmel, die Ergebnisse beim Würfeln mit Freunden, die Darstellung des DAX über dem Frankfurter Börsenparkett. Ist Zufall aber immer eindeutig zu identifizieren? Was denken Sie, welche der folgenden Zahlenreihen sind zufällig?
A: 0,8443; 0,1458; 0,3509; 0,0402; 0,1151; 0,4171; 0,6100; 0,2207; 0,4025; 0,7929; ...
B: 0,1000; 0,0000; 0,3000; 0,4000; 0,1000; 0,0000; 0,3000; 0,4000; 0,1000; 0,0000; ...
C: 0,0620; 0,9547; 0,3858; 0,3553; 0,8633; 0,9098; 0,4947; 0,6181; 0,2800; 0,4803; ...
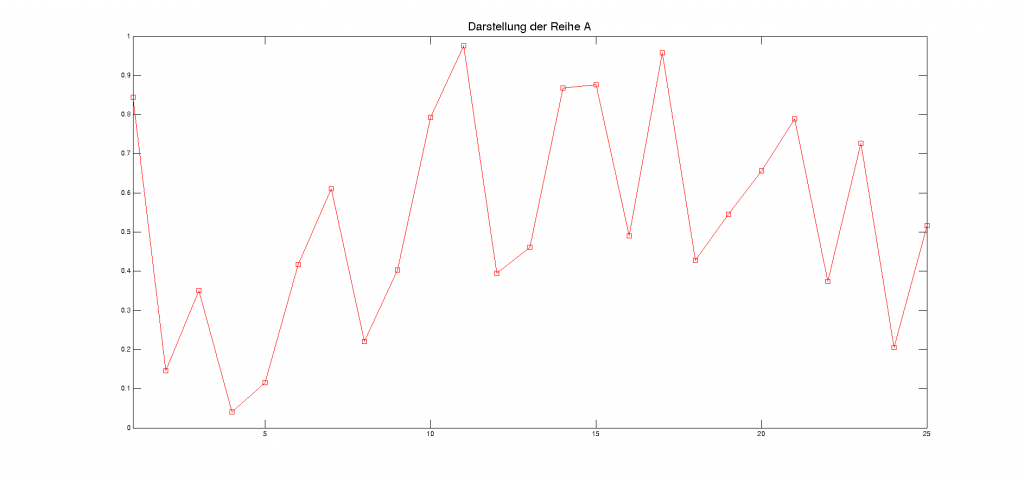
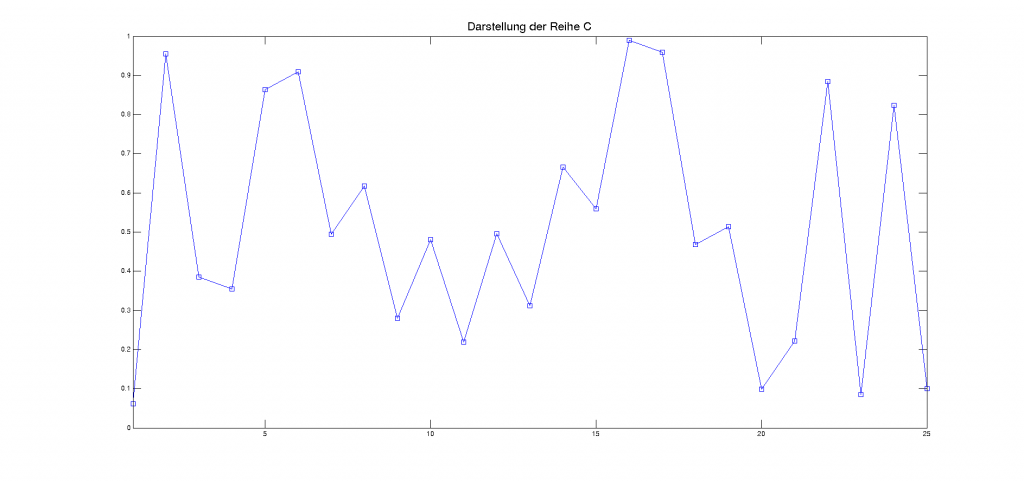
Es ist einfach zu sehen, dass die Reihe B nicht zufällig ist. Die Zahlen 0,1; 0,0; 0,3; 0,4 wiederholen sich. Was ist aber mit den Reihen A und C? Vielleicht hilft es, wenn wir diese Zahlenreihen als Graph mit 25 anstatt 10 Werten auftragen. Betrachten Sie dazu die folgenden Abbildungen (Werte sind als kleine Quadrate eingezeichnet, die durch Linien miteinander verbunden sind). Was denken Sie, sind das zufällige Verläufe, oder nicht?
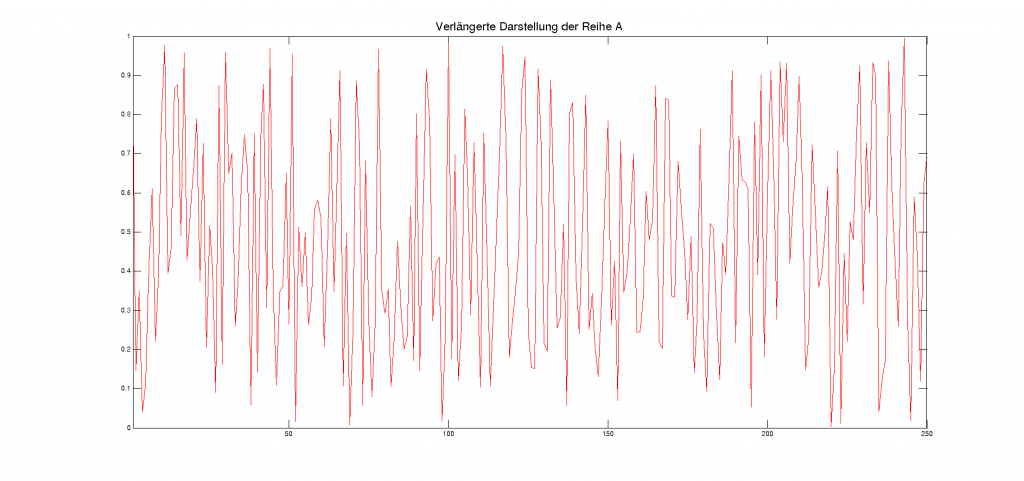
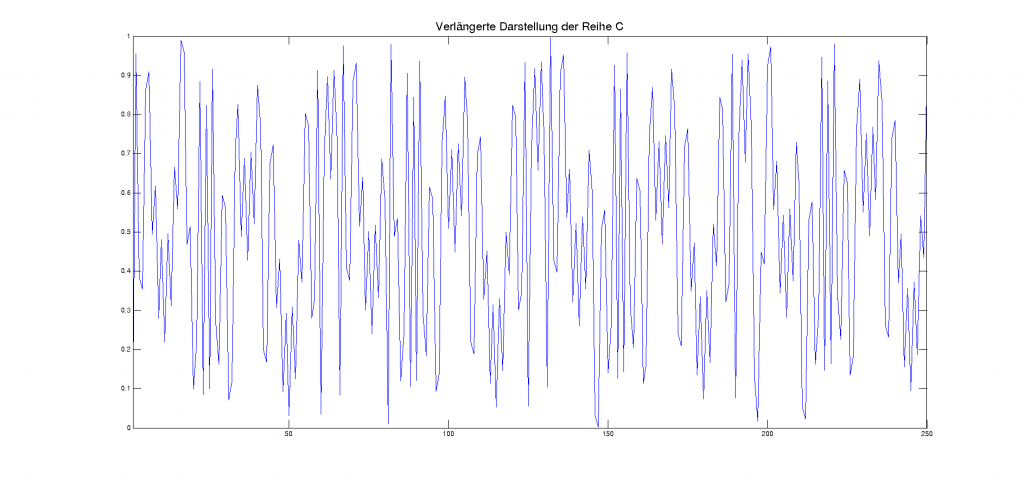
Über diese Darstellung festzustellen ob eine der beiden Reihen aus zufälligen Werten besteht ist wohl nicht möglich. Anders sieht es aus, wenn noch mehr Werte der Reihe in das Diagramm eingetragen werden. Die folgenden Abbildungen umfassen die ersten 250 Werte der Reihen A und C.
Die Zahlen aus der Reihe A sind in der Tat zufällige Werte. Sie stammen aus dem atmosphärischen Rauschen und werden durch die Seite Random.org zur Verfügung gestellt [1].
Bei genauer Betrachtung sind bei der Reihe C gewisse Muster zu erkennen (Schauen Sie sich z.B. dazu den M-artigen Zacken nach unten zu Beginn an und vergleichen ihn mit dem ähnlichen Muster an der Stelle 50). Dies liegt daran, dass diese Zahlenreihe durch einen Zufallszahlengenerator erzeugt wurde und damit nicht "richtig zufällig" ist. Aus diesem Grund ist Pseudozufallszahlengenerator der eigentlich korrekte Begriff. Es gibt verschiedene Typen derartiger Generatoren. Das Beispiel C wurde mit einem sogenannten linearen Kongruenzgenerator erzeugt, einem sehr bekannten und aber nur eingeschränkt nutzbarem Typ (siehe auch in diesem Blog: Komplizierter Name, einfache Funktion: Der lineare Kongruenzgenerator). Dieser hat, was die Güte der Zufallszahlen betrifft, also wie zufällig die Zahlen erscheinen, große Schwächen. Noch offensichtlicher wird dies, wenn man die Reihe C auf eine andere Weise in ein Diagramm einträgt.
Hyperebenen
In einem dreidimensionalen Diagramm gibt es die drei Achsen x, y und z. Ein Punkt ist hier eindeutig durch die Angabe der drei Werte für x, y und z definiert. Nimmt man nun die Zahlenreihe C des Pseudozufallszahlengenerators und vergibt für x den ersten, für y den zweiten und für z den dritten Wert der Zahlenreihe so erhält man den ersten Punkt eines Diagramms. Anschließend geht man eine Zahl in der Reihe weiter und bildet auf die gleiche Art den zweiten Diagrammpunkt. Ebenso verfährt man für alle weiteren Punkte, bis die Reihe zu Ende ist. In unserem Beispiel wäre der erste Punkt
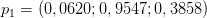
und der zweite
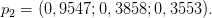
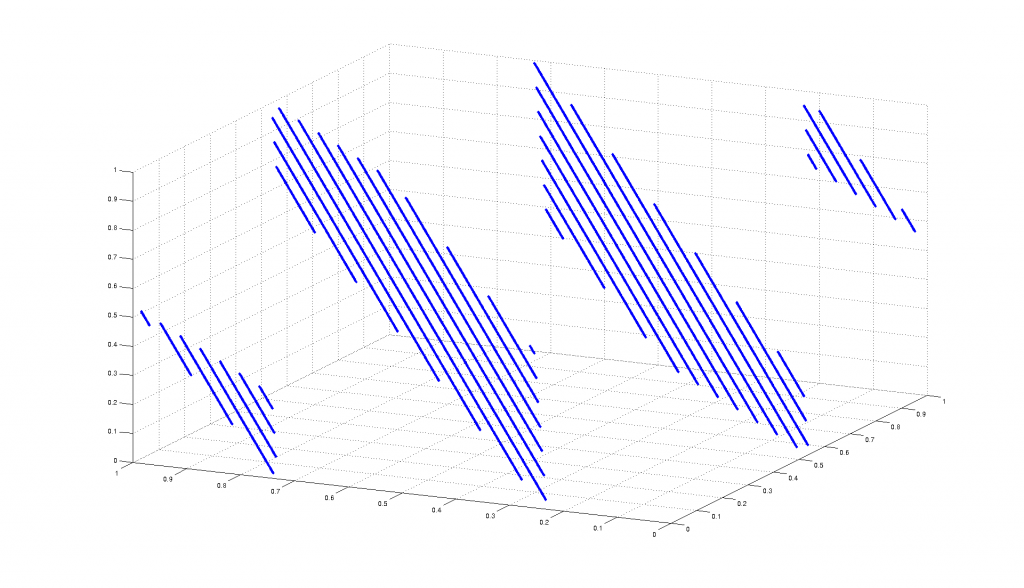
In den Klammern steht zunächst der x-, dann der y- und schließlich der z-Wert. Das dreidimensionale, grafische Ergebnis sieht dann wie folgt aus.
In dieser Grafik ist zu sehen, dass sich die bisher einigermaßen zufällig aussehenden Zahlen in einem sehr regelmäßigen Muster anordnen. In der dreidimensionalen Darstellung bilden sich quasi Flächen von Punkten, die Hyperebenen genannt werden.
Zufall in verschiedenen Güteklassen
Die Qualität von Pseudozufallszahlengeneratoren ist für viele Anwendungen, insbesondere wenn es um sicherheitsrelevante Kryptographiesysteme geht, entscheidend. Systeme die einfach vorherzusehende Pseudozufallszahlen verwenden sind sehr viel leichter zu knacken. Die oben dargestellten Hyperebenen sind nur eine einfache und anschauliche Art die Regelmäßigkeit eines Pseudozufallszahlengenerators zu betrachten. Darüber hinaus gibt es verschiedene Testverfahren für Generatoren, mit denen die Güte festgestellt werden kann.
Für Felix Magath ist hingegen wohl nur eine Messgröße für die Qualität von Bedeutung: Tore!
Referenzen
[1] Random.org, 2013: Random Integer Generator. URL: https://www.random.org/integers (18.12.2013)