Im Rahmen des 117. Deutschen Ärztetages Ende Mai veröffentlichte die Berliner Zeitung ein Interview mit Frank Ulrich Montgomery, dem Präsidenten der Bundesärztekammer [1]. In dem Gespräch betont Montgomery, der ebenfalls erster Vorsitzender des Marburger Bundes ist, dass bei Vorsorgeuntersuchungen stärker auf Nutzen und Risiken geachtet werden müsse. Der Hinweis des Ärztepräsidenten ist richtig und wichtig. Denn allein die mathematisch eingehende Betrachtung von Wahrscheinlichkeiten bei Krebsvorsorgeuntersuchungen dürfte für viele Patienten vollkommen überraschend sein.
Brustkrebs und Mammographien
Brustkrebs bei Frauen tritt mit einer Prävalenz (Krankheitshäufigkeit in einer bestimmten Gruppe) von etwa 1% auf [2]. Als Vorsorgeuntersuchung bieten Mediziner die Mammographie an. Dabei werden Röntgenbilder der weiblichen Brust aus verschiedenen Richtungen aufgenommen. Sollte die Patientin wirklich an Brustkrebs erkrankt sein, so wird dies in etwa 90% der Fälle durch das Screening richtig erkannt. Diese Quote wird in der Statistik Sensitivität genannt. Sollte die Frau nicht an Brustkrebs erkrankt sein, so wird dies in ungefähr 95% der Fälle durch die Mammographie richtig festgestellt. Diese Größe bezeichnet man als Spezifität. Diese hohen Zahlen, die von verschiedenen Faktoren abhängen und auch etwas schwanken können [3, 4], überzeugen vordergründig auf den ersten Blick und scheinen in überwältigendem Maße für das Screening zu sprechen. Die entscheidende Frage ist jedoch, wie hoch ist die Wahrscheinlichkeit an Brustkrebs erkrankt zu sein, wenn der Test dieses Ergebnis hervorbringt? Die Patientin weiß es vor dem Test ja nicht und erhofft sich einen Erkenntnisgewinn durch die Untersuchung.
Wahrscheinlichkeiten nach Thomas Bayes
Die Situation ist klar: Es gibt eine Wahrscheinlichkeit für ein gewisses Ereignis und ein dafür vorgesehener Test soll zur Klarheit verhelfen. Um diesen Sachverhalt nicht nur aus dem Bauch heraus zu beurteilen müssen, nimmt man einen mathematischen Zusammenhang zur Hilfe, der auf den Briten Thomas Bayes (1701-1761), einem presbyterianischen Pfarrer und Mathematiker, zurückgeht [5].
Dieses sogenannte Bayes-Theorem beschreibt die Berechnung von bedingten Wahrscheinlichkeiten, also die Frage wie wahrscheinlich A ist, wenn B bereits eingetreten ist. Diese Wahrscheinlichkeit wird in der üblichen mathematischen Schreibweise 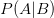 geschrieben. Zu lesen ist dieser Ausdruck demnach so: Die Wahrscheinlichkeit
geschrieben. Zu lesen ist dieser Ausdruck demnach so: Die Wahrscheinlichkeit  , dass das Ereignis
, dass das Ereignis 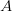 eintritt, wenn das Eintreten des Ereignisses
eintritt, wenn das Eintreten des Ereignisses  bereits bekannt ist. Dieser Begriff kann auch in der Frage des Brustkrebs-Screenings angewendet werden. Wie hoch ist die Wahrscheinlichkeit
bereits bekannt ist. Dieser Begriff kann auch in der Frage des Brustkrebs-Screenings angewendet werden. Wie hoch ist die Wahrscheinlichkeit  an Brustkrebs erkrankt zu sein - was mit
an Brustkrebs erkrankt zu sein - was mit 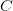 ausgedrückt werden soll - wenn die Untersuchung ein positives Ergebnis, bezeichnet mit
ausgedrückt werden soll - wenn die Untersuchung ein positives Ergebnis, bezeichnet mit 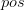 , also einen Krebsbefund ausstellt:
, also einen Krebsbefund ausstellt: 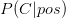
Das Bayes-Theorem im Einzelnen
Nach dem Bayes-Theorem lässt sich diese Wahrscheinlichkeit über die Formel
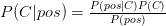
berechnen. Wir wollen diese Formel Stück für Stück verstehen. Über dem Bruchstrich steht zum einen die Wahrscheinlichkeit, einen Krebsbefund durch die Untersuchung zu erhalten, wenn die Patientin in der Tat an Krebs erkrankt ist 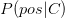 . Dies ist die bereits oben angesprochene Sensitivität des Tests. Diese ergibt sich aus medizinischen Statistiken der Vergangenheit und bezieht sich nicht auf den gerade untersuchten Fall. Es ist wichtig zu verstehen, dass dies nicht dasselbe ist, wie die Wahrscheinlichkeit für Krebs bei einem zuvor bekannt gewordenen positiven Testergebnis.
. Dies ist die bereits oben angesprochene Sensitivität des Tests. Diese ergibt sich aus medizinischen Statistiken der Vergangenheit und bezieht sich nicht auf den gerade untersuchten Fall. Es ist wichtig zu verstehen, dass dies nicht dasselbe ist, wie die Wahrscheinlichkeit für Krebs bei einem zuvor bekannt gewordenen positiven Testergebnis.
Der zweite Faktor über dem Bruchstrich ist die einfache Wahrscheinlichkeit dafür überhaupt an Krebs zu erkranken 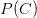 . Damit ist diese Wahrscheinlichkeit die bereits angesprochene Krankheitshäufigkeit bzw. Prävalenz.
. Damit ist diese Wahrscheinlichkeit die bereits angesprochene Krankheitshäufigkeit bzw. Prävalenz.
Schließlich bleibt noch der Ausdruck 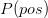 unter dem Bruchstrich. Er drückt die Gesamtwahrscheinlichkeit für ein positives Testergebnis aus, ganz gleich, ob die untersuchte Patientin an Krebs erkrankt ist oder nicht. Wie wir bereits oben gesehen haben, kann nämlich auch eine gesunde Patientin einen Krebsbefund ausgestellt bekommen.
unter dem Bruchstrich. Er drückt die Gesamtwahrscheinlichkeit für ein positives Testergebnis aus, ganz gleich, ob die untersuchte Patientin an Krebs erkrankt ist oder nicht. Wie wir bereits oben gesehen haben, kann nämlich auch eine gesunde Patientin einen Krebsbefund ausgestellt bekommen.
Berechnung der Krebswahrscheinlichkeit nach positivem Test
Wir wollen nun alle Teile der Formel berechnen und damit herausfinden, wie hoch die Wahrscheinlichkeit für Krebs bei einem positiven Befund wirklich ist. Die Wahrscheinlichkeit für Brustkrebs (Prävalenz) lag bei 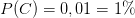 (Abb. 2). Die Sensitivität geht mit
(Abb. 2). Die Sensitivität geht mit 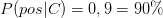 ein.
ein.

Abb. 3: Von 1000 Patientinnen erhalten ca. 59 ein positives Testergebnis. Damit sind sowohl gesunde wie auch erkrankte Patientinnen betroffen.

Abb. 2: Brustkrebs tritt mit einer Häufigkeit von ca. 1% auf. Damit sind von 1000 Frauen etwa zehn von der Krankheit betroffen.
Die Gesamtwahrscheinlichkeit eines positiven Testergebnisses besteht aus der Summe der Produkte der Wahrscheinlichkeiten 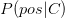 und
und 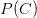 , die wir bereits beide kennen, sowie
, die wir bereits beide kennen, sowie  und
und 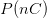 , wobei
, wobei 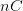 ein negatives Ergebnis, also keine Krebserkrankung ausdrücken soll. Der Fall eines positiven Testresultats bei fehlender Erkrankung wird falsch negativer Befund genannt. Wenn mit der Spezifität insgesamt 95% der Tests korrekterweise negativ ausfallen (Krebserkrankung liegt nicht vor) dann fallen auf der anderen Seite damit 5% positiv aus (sog. falsch positiver Befund), obwohl dies nicht stimmt.
ein negatives Ergebnis, also keine Krebserkrankung ausdrücken soll. Der Fall eines positiven Testresultats bei fehlender Erkrankung wird falsch negativer Befund genannt. Wenn mit der Spezifität insgesamt 95% der Tests korrekterweise negativ ausfallen (Krebserkrankung liegt nicht vor) dann fallen auf der anderen Seite damit 5% positiv aus (sog. falsch positiver Befund), obwohl dies nicht stimmt.
Schließlich ist die generelle Wahrscheinlichkeit nicht an Krebs erkrankt zu sein 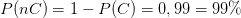 Damit ist
Damit ist 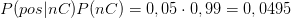 . Damit ist die Gesamtwahrscheinlichkeit für einen positiven Befund
. Damit ist die Gesamtwahrscheinlichkeit für einen positiven Befund
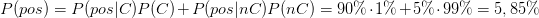
Die Wahrscheinlichkeit von 5,85% für einen positiven Befund ist in Abbildung 3 beispielhaft dargestellt. Dort haben von 1000 Frauen 59 einen Krebsbefund erhalten. Wir können nun abschließend berechnen, wie hoch die Wahrscheinlichkeit ist, an Krebs erkrankt zu sein, wenn die Patientin ein positives Screening-Ergebnis erhalten sollte.
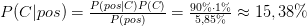
Fassen wir zusammen: Vor der Untersuchung liegt die Wahrscheinlichkeit an Brustkrebs erkrankt zu sein durch die allgemeine Häufigkeit dieser Krankheit bei 1%. Erhält die Patientin aufgrund des Screenings die Diagnose Brustkrebs, so steigt die Wahrscheinlichkeit, wirklich an Krebs erkrankt zu sein, auf lediglich etwa 15%. Es ist mitnichten so, dass ein positiver Mammographiebefund automatisch eine sichere Krebsdiagnose ist.
Auswirkungen falsch verstandener Wahrscheinlichkeiten
Dieser Zusammenhang ist von erheblicher Bedeutung. Es ist wichtig Patientinnen über diesen im Kern mathematischen Umstand korrekt aufzuklären. Ohne Frage ist positiv hervorzuheben, dass eine tatsächliche Krebserkrankung auch mit sehr hoher Wahrscheinlichkeit vom Screening erkannt wird. Im vorgestellten Beispiel lag diese bei 90%. Dies darf aber nicht zu Fehlinterpretationen führen. Es ist durchaus nicht unwahrscheinlich, dass eine nicht an Brustkrebs erkrankte Frau einen positiven Mammographiebefund erhält. Durch eine detaillierte Aufklärung können auf diese Weise negative psychische Auswirkungen mit erheblichem Ausmaß reduziert werden.
Die von Frank Ulrich Montgomery angeregte kritische Betrachtung von Vorsorgeuntersuchungen ist daher auch im Hinblick auf das Patienten- und Aufklärungsgespräch berechtigt. Zum besseren Verständnis der Patientinnen und Patienten sollte eine relativ einfache mathematische Beziehung aus dem 18. Jahrhundert wie das Bayes-Theorem Teil von medizinischen Vorlesungen und klinischen Untersuchungen des 21. Jahrhunderts sein.
Referenzen
[1] Timot Szent-Ivanyi, Frank Ulrich Montgomery, 2014: „Kommt uns nicht mit der Moralkeule“. Berliner Zeitung. URL: http://www.berliner-zeitung.de/wirtschaft/aerztepraesident-montgomery--kommt-uns-nicht-mit-der-moralkeule-,10808230,27228254.html (23.06.2014)
[2] Robert Koch-Institut, 2010: Verbreitung von Krebserkrankungen in Deutschland. Berlin, S. 77. URL: http://www.bmg.bund.de/fileadmin/dateien/Downloads/K/Krebs/Nationaler_Krebsplan/Krebspraevalenz.pdf (23.06.2014)
[3] L. E. M. Duijm, et al., 1997: Sensitivity, specificity and predictive values of breast imaging in the detection of cancer. Britisch Journal of Cancer 76 (3), S. 377-381
[4] A. M. Kavanagh, G. G. Giles, H. Mitchell, J. N. Cawson, 2000: The sensitivity, specificity, and positive predictive value of screening mammography and symptomatic status. J Med Screen 7 (2), S. 105-110.
[5] Thomas Bayes, Richard Price, 1763: An Essay towards solving a Problem in the Doctrine of Chance. By the late Rev. Mr. Bayes, communicated by Mr. Price, in a letter to John Canton, A. M. F. R. S. Philosophical Transactions of the Royal Society of London 53 (0), S. 370-418. URL: http://rstl.royalsocietypublishing.org/content/53/370 (23.06.2014)


