"Wir ertrinken in Informationen, aber hungern nach Wissen."
John Naisbitt (*1929), US-amerikanischer Zukunftsforscher
Datenalltag
In allen Lebensbereichen steigt die Bedeutung von Informationen, Daten und Modellen. Dies bedeutet jedoch nicht, dass auch allen das damit verbundene Wissen zugänglich ist. Konzepte, Methoden und Verfahren zur Auswertung von riesigen Datenmengen sind komplex und entwickeln sich ständig weiter. Es ist nicht einfach die Hintergründe dieser Analysen und Anwendungen zu verstehen, insbesondere für die breite Öffentlichkeit. Trotzdem sieht sich jeder Bürger verstärkt mit Schlagworten wie Risikomodelle, Systemversagen, Big Data, Mailverschlüsselung und Cyberkrieg konfrontiert. In der modernen Welt beschleunigt sich die Technisierung sowie Mathematisierung und ehemals klare Grenzen verschwimmen. So sind Datenerhebungen über Freizeitverhalten genauso selbstverständlich geworden wie eine naturwissenschaftlich anmutende Formelsprache und Modellbildung im Wirtschafts- und Sozialleben. Ob dies sinnvoll und zielführend ist, ist von Fall zu Fall verschieden und sei erstmal dahingestellt.
Damit sind Menschen nicht nur Konsumenten sondern in vielen Fällen auch direkt beteiligt. Soziale Netzwerke erheben die Daten ihrer Mitglieder und erwirtschaften damit Profit. An der Börse wird ein Computerhandel in Bruchteilen von Sekunden abgewickelt. Das Verhalten von Verbrauchern und ganzen Volkswirtschaften wird mathematisch analysiert und modelliert. Kommunikation findet über Mobiltelefone und Computer zu jeder Zeit und an jedem Ort statt. Repräsentative Umfragen versuchen den Wahlausgang vorherzusagen. Unmittelbar nach einem Spiel in der Fußball-Bundesliga werden Statistiken und Analysen zu Passquoten und Laufwegen präsentiert.

Ziel des Blogs
Dieser Blog bewegt sich an den Schnittstellen von Naturwissenschaft (insbesondere Mathematik und Physik), Wirtschaft, Politik und Datenverarbeitung sowie -aufbereitung. Die Themen sollen dabei nicht akademisch abgearbeitet werden. Vielmehr ist es das Ziel dieses Blogs, Inhalte für eine breite Leserschaft aufzubereiten und verständlich zu machen. Zentrales Anliegen ist es, einige dieser Konzepte, Zusammenhänge und Verfahren eingehender aber nachvollziehbar zu erklären. Dabei soll bewusst auf einfache Formeln nicht verzichtet werden, da ihre Bedeutung auch im täglichen Wirtschaftsleben stetig zunimmt. Der Anspruch dieses Blogs ist es daher auch, dem ungeübten Leser diese Formelsprache näher zu bringen und dadurch mündiger in einer durch Statistiken, Analysen und Modellen geprägten (und teilweise überfrachteten) Welt zu werden.
Warum heißt der Blog Attraktor?
Der Begriff findet unter anderem bei der Beschreibung von physikalischen Systemen Anwendung. Stellen Sie sich ein Metronom (Taktmesser) vor, das in einer Ebene von links nach rechts und wieder zurück schwingt. Ein Betrachter kann diese Bewegung mit dem Auge nachvollziehen. Zu einem bestimmten Zeitpunkt befindet sich die Spitze an einem ganz bestimmten Ort und hat eine ganz bestimmte Geschwindigkeit. Etwas später befindet es sich an einer anderen Stelle und ist zum Beispiel langsamer oder schneller. Der Beobachter kann den Ort der Spitze relativ genau erkennen. Die Geschwindigkeit hingegen kann er ohne weitere Hilfsmittel nur abschätzen und wie Ort und Geschwindigkeit zusammenhängen ist einen weiteren Gedankenschritt entfernt.
In diesem Beispiel sind der Aufenthaltsort der Metronomspitze und ihre Geschwindikeit zwei Systemzustände. Diese Zustände lassen sich in einem Diagramm auftragen, so wie es die folgende Abbildung zeigt.
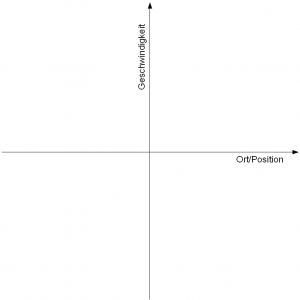 Diese Fläche, die natürlich bei mehr als zwei Zuständen auch ein Raum sein kann, wird Zustands- oder Phasenraum genannt. Bei einer entsprechenden Einstellung wird das Metronom immer im Takt zwischen den zwei Extremausschlägen hin und her schwingen, auch wenn Sie es zuvor stärker ausgelenkt haben. Die Zustände - also die möglichen Aufenthaltsorte und Geschwindigkeiten der Metronomspitze - auf die sich das Metronom trotz größerer anfänglicher Auslenkung immer einpendelt, sind der Attraktor des Metronom-Systems. In diesem speziellen Beispiel wäre das ein Kreis, der alle möglichen Kombinationen von Ort und Geschwindigkeit markiert.
Diese Fläche, die natürlich bei mehr als zwei Zuständen auch ein Raum sein kann, wird Zustands- oder Phasenraum genannt. Bei einer entsprechenden Einstellung wird das Metronom immer im Takt zwischen den zwei Extremausschlägen hin und her schwingen, auch wenn Sie es zuvor stärker ausgelenkt haben. Die Zustände - also die möglichen Aufenthaltsorte und Geschwindigkeiten der Metronomspitze - auf die sich das Metronom trotz größerer anfänglicher Auslenkung immer einpendelt, sind der Attraktor des Metronom-Systems. In diesem speziellen Beispiel wäre das ein Kreis, der alle möglichen Kombinationen von Ort und Geschwindigkeit markiert.
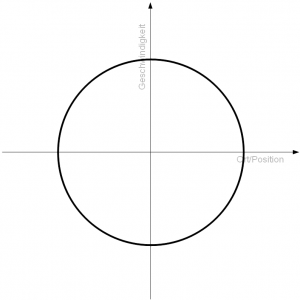
In der Mitte, wenn der Taktgeber ertönt, ist das Metronom am schnellsten. Dies sind im Zustandsraumdiagramm die Schnittpunkte des Kreises mit der senkrechten Achse. An den beiden Extrempunkten, an denen das Metronom die Richtung ändert, besitzt es kurzzeitig keine Geschwindigkeit. Dies entspricht den Schnittpunkten des Kreises mit der waagerechten Achse. Das oben gezeigte Diagramm macht nun den Zusammenhang von Ort und Geschwindigkeit sichtbar. Damit wird durch den Attraktor die gesamte Bewegung des Metronoms in ihren Einzelheiten anschaulicher.
Zustände können aber nicht nur der Aufenthaltsort oder die Geschwindigkeit eines Systems sein. Auch die Temperatur, der Luftdruck oder die elektrische Ladung sowie abstrakte Größen ohne physikalisch-erfahrbare Bedeutung können als Zustände aufgefasst werden.
Es gibt nun Systeme, deren wie auch immer geartete Zustände sich auf chaotische Weise ändern. Oftmals sehen diese Änderungen rein zufällig (stochastisch) aus. Allerdings handelt es sich bei diesen Mechanismen um Systeme, die sich exakt nach einer oder mehrerer Gleichungen entwickeln und somit überhaupt nicht zufällig sind. Man spricht dann von deterministischen Systemen. Auch dieses chaotische Verhalten kann durch Attraktoren dargestellt werden, die allerdings sehr unterschiedliche Formen annehmen können und daher seltsamer Attraktor heißen. In der folgenden Abbildung ist ein Beispiel dafür gezeigt.

Ein chaotisches und zufällig wirkendes System kann somit durchaus eine tiefgreifende Systematik besitzen, welche durch einen Attraktor anschaulich gemacht wird. Von komplizierten und unübersichtlichen Strukturen etwas über die grundlegende Ordnung zu erfahren, darum soll es in diesem Blog gehen.
Kontakt
Haben Sie Fragen, Anregungen, Kritik? Bitte sende Sie eine Mail an: blog{at}attraktor.info
