Eine grafische Darstellung einer Ungleichverteilung von Einkommen ist die Lorenz-Kurve, die wir im zweiten Teil der Reihe zur Vermessung der Ungleichheit betrachtet hatten. Sie kann jedoch als grafisches Verfahren nicht direkt exakte Ergebnisse liefern. Es gibt jedoch eine Indexgröße, die auf diesem Verfahren aufbaut und als Ergebnis eine Zahl liefert, die Ungleichverteilungen besser vergleichbar machen soll. Hierbei handelt es sich um den Gini-Koeffizienten, der im Fokus des dritten Teils der Reihe zu Ungleichverteilungen steht.
Gini-Koeffizient als Fläche unter der Lorenz-Kurve
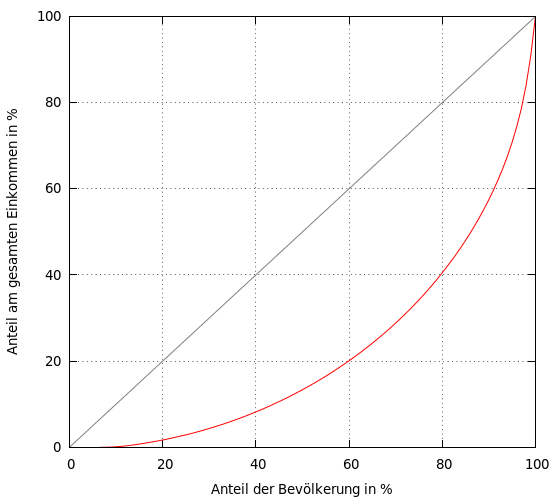
Abb. 1: Lorenzkurve (rot) einer Ungleichverteilung (Gleichverteilung in grau)
Mit Blick auf die Lorenz-Kurve erinnern wir uns an die Wölbung, die das Maß der Ungleichverteilung ausdrückte (siehe Abb. 1). Je stärker die Kurve gewölbt ist, umso weniger gleich verteilt ist zum Beispiel das Einkommen innerhalb einer Population. Erhält nur eine Person der Bevölkerung das gesamte Einkommen, so liegt der Extremfall der vollständigen Ungleichverteilung vor. In diesem Fall verläuft die Lorenzkurve auf der waagerechten Achse, um schließlich beim letzten Wert sprunghaft auf 100% zu springen. Um die grafische Aussage zu quantifizieren, werden nach Corrado Gini (1884-1965), einem italienischen Soziologen und Statistiker, die Flächen in Relation gesetzt, die unter dem Graphen der absoluten Gleichverteilung sowie der Lorenz-Kurve liegen [1].
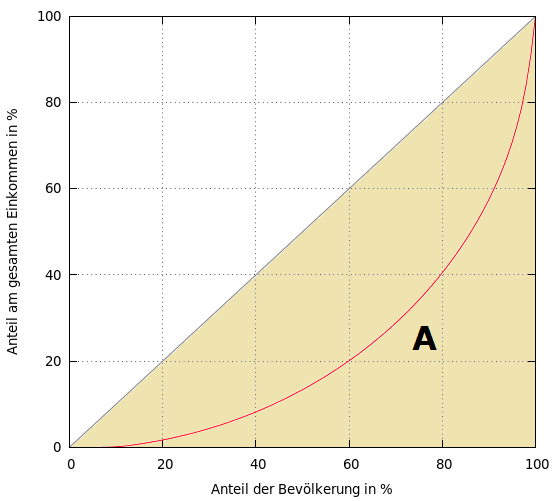
Abb. 2: Fläche unter der Linie der totalen Gleichverteilung
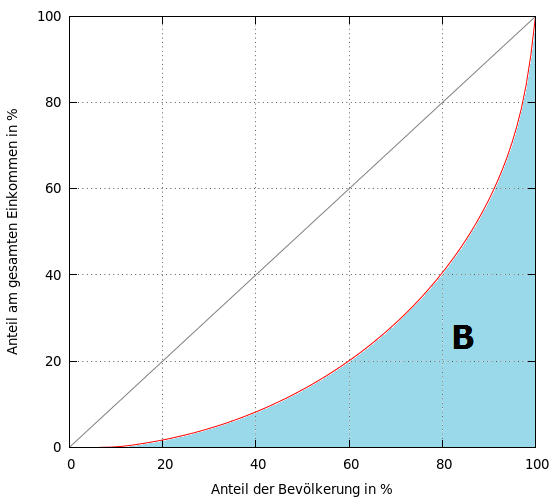
Abb. 3: Fläche unter der Lorenz-Kurve
Betrachten wir hierzu die folgende Abbildungen 2 und 3. Es handelt sich dabei um die gleiche Lorenz-Kurve wie in der ersten Abbildung. Zu sehen ist jetzt die Fläche 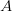 , die unterhalb der Linie der vollkommenen Gleichverteilung (grau) liegt (Abb. 2). Entsprechend handelt es sich bei der Fläche
, die unterhalb der Linie der vollkommenen Gleichverteilung (grau) liegt (Abb. 2). Entsprechend handelt es sich bei der Fläche  um diejenige, die durch die Lorenz-Kurve nach oben abgegrenzt wird (Abb. 3).
um diejenige, die durch die Lorenz-Kurve nach oben abgegrenzt wird (Abb. 3).
Werden diese Flächen nun in ein mathematisches Verhältnis gesetzt, lässt sich ein Index berechnen, der eine quantitative Aussage über die Ungleichverteilung möglich macht. Der Gini-Koeffizient 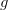 berechnet sich daher über die Formel
berechnet sich daher über die Formel
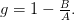
Extremfälle
Um die Formel besser zu verstehen, sehen wir uns die Extremfälle genauer an. Beginnen wir mit der vollkommenen Gleichverteilung. Hierbei liegt die Lorenzkurve genau auf der Diagonalen. Damit sind die Flächen 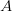 und
und  identisch, also gleich groß (
identisch, also gleich groß (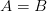 ). Setzt man dies in die Formel für den Gini-Koeffizienten ein, erhält man als Ergebnis 0.
). Setzt man dies in die Formel für den Gini-Koeffizienten ein, erhält man als Ergebnis 0.
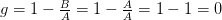
Ein Gini-Koeffizient von 0 beschreibt demnach die perfekte Gleichverteilung von zum Beispiel Einkommen und ist darüber hinaus auch der kleinstmögliche Wert des Index. Der größtmögliche Wert wird bei maximaler Ungleichverteilung erreicht. Dieser Fall wurde durch die waagerecht verlaufende Lorenz-Kurve mit abschließendem Anstieg auf 100% beschrieben. Dementsprechend existiert keine weitere Fläche unter der Lorenz-Kurve und es gilt demnach 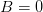 . Auch diesen Wert setzen wir in die Formel ein.
. Auch diesen Wert setzen wir in die Formel ein.
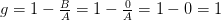
Eine vollständige Ungleichverteilung wird durch einen Gini-Koeffizienten von 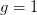 beschrieben. Der Gini-Koeffizient liegt daher immer im Intervall zwischen 0 und 1, außer er wird auf größere Werte hochskaliert, zum Beispiel auf das Intervall 0 bis 100. Dies ändert aber an der grundlegenden Aussage nichts.
beschrieben. Der Gini-Koeffizient liegt daher immer im Intervall zwischen 0 und 1, außer er wird auf größere Werte hochskaliert, zum Beispiel auf das Intervall 0 bis 100. Dies ändert aber an der grundlegenden Aussage nichts.
Beispiele für Gini-Koeffizienten
In welchem Bereich bewegen sich reale Gini-Koeffizienten? Dazu wollen wir uns ein paar ausgewählte Nationen und ihre Gini-Koeffizienten zum Familieneinkommen [2] in der folgenden Tabelle ansehen.
- Deutschland: 0,27 (2006)
- Frankreich: 0,33 (2008)
- Japan: 0,38 (2008)
- Großbritannien: 0,40 (2009)
- Russland: 0,42 (2011)
- USA: 0,45 (2007)
In dieser kurzen Liste einiger Nationen besitzt Deutschland den geringsten Gini-Koeffizienten und würde demnach das Familieneinkommen im Verhältnis zu den anderen Nationen relativ gleichverteilen. In den USA hingegen läge eine größere Ungleichverteilung als in allen anderen Staaten der Liste vor. Statistiken zum Gini-Koeffizienten sind jedoch immer vorsichtig zu behandeln. Im Beispiel ist auch zu sehen, dass durchgängige Werte zu einem Jahr nicht zu ermitteln waren [3]. Auch ist nicht mit absoluter Sicherheit zu sagen, ob die verschiedenen Indizes mit der gleichen Systematik und auf vergleichbaren Berechnungsgrundlagen kalkuliert wurden.
Darüber hinaus können verschiedene Ungleichverteilungen - ähnlich wie bei der Lorenz-Kurve - den gleichen Gini-Koeffizienten besitzen. Dazu muss einzig die Fläche  in beiden Fällen gleich groß sein. Schließlich sind Gini-Koeffizienten für eine angemessene Interpretation auch in ihrer zeitlichen Entwicklung zu betrachten, da sich demografische Faktoren auf den Index auswirken können.
in beiden Fällen gleich groß sein. Schließlich sind Gini-Koeffizienten für eine angemessene Interpretation auch in ihrer zeitlichen Entwicklung zu betrachten, da sich demografische Faktoren auf den Index auswirken können.
Lesen Sie hierzu auch/demnächst...
Der Theil-Index (demnächst)
Referenzen
[1] Corrado Gini, 1912: Variabilità e Mutuabilità. Contributo allo Studio delle Distribuzioni e delle Relazioni Statistiche. C. Cuppini, Bologna
[2] Central Intelligence Agency (CIA), 2014: The World Factbook, Distribution of family income - Gini index. URL: https://www.cia.gov/library/publications/the-world-factbook/fields/2172.html#gm (17.03.2014)
[3] The World Bank, 2014: GINI index. URL: http://data.worldbank.org/indicator/SI.POV.GINI (17.03.2014)
