Die Anwendungen, in denen Zufallszahlen gebraucht werden, sind mannigfaltig. Theoretisch fallen Zufallszahlen sogar von Himmel: Das atmosphärische Rauschen ist ein Beispiel für einen physikalischen Zufallsgenerator. Allerdings sind oftmals praktischere Softwarelösungen erforderlich. Eine der einfachsten Formen um Zufallszahlen - die in Wirklichkeit keine sind, aber oberflächlich so aussehen - zu generieren ist der lineare Kongruenzgenerator (engl. linear congruential generator, LCG). Hinter diesem schwierigen Namen verbirgt sich eine relativ einfache mathematische Vorschrift.
Math around the clock
Niemand wundert sich darüber, dass nach 23:00 Uhr eine Stunde später 0:00 Uhr folgt. Die Zeitmessung auf diesem Planeten funktioniert nun einmal in wiederkehrenden Intervallen. Oftmals ist aus der Grundschulzeit hingegen eine ähnlich intervallartige Rechenart in Vergessenheit geraten. Im Rechenunterricht lernten wir das schriftliche Dividieren. Manchmal kam dabei ein Rest heraus, zumindest so lange, wie uns mathematische Brüche unbekannt waren. Die Rechnung 5 geteilt durch 2 ergab eben 2 mit Rest 1 und nicht 2,5. Die Berechnung des Rests wird in der Mathematik als Modulo bezeichnet, mit mod abgekürzt und erzeugt Ergebnisse, die sich ähnlich wie bei der Uhrzeit ständig wiederholen.
0 mod 2 = 0 (0 geteilt durch 2 ist gleich 0 mit Rest 0)
1 mod 2 = 1 (1 geteilt durch 2 ist gleich 0 mit Rest 1)
2 mod 2 = 0 (2 geteilt durch 2 ist gleich 1 mit Rest 0)
3 mod 2 = 1 (3 geteilt durch 2 ist gleich 1 mit Rest 1)
usw.
In diesem Beispiel kennt die Uhr nur zwei Uhrzeiten und wiederholt sich demnach immer nach dem Intervall 0 und 1. Möchte man die 24 Stunden des Tages nachbilden, würde man Modulo 24 rechnen und erhielte alle Uhrzeiten von 0:00 bis 23:00 Uhr. Aus diesem Grund wird dieses Verfahren manchmal auch Uhrenmathematik genannt. Aber was hat die Uhrzeit mit der Generierung von (Pseudo-)Zufallszahlen oder gar dem linearen Kongruenzgenerator zu tun?
Fließbandproduktion von Pseudozufallszahlen
Mit der Modulorechnung haben wir schon den schwierigsten Teil der Rechnenweise eines linearen Kongruenzgenerators verstanden. Sie sorgt dafür, dass die generierten Zufallszahlen auf ein bestimmtes Intervall begrenzt sind und so aussehen, als würden die Werte zufällig hin und her springen. Ansonsten gibt es in der Rechenvorschrift des Kongruenzgenerators nur noch eine Multiplikation und Addition auszuführen. Zunächst aber legen wir ein paar Werte fest, die bis auf den Startwert (oder engl. seed) die ganze Zeit unverändert bleiben:
- Man wählt einen Startwert, z.B. 4.
- Als nächstes wählt man sich einen Faktor, der für die gesamte Zeit konstant bleibt, z.B. 3.
- Auch ein Inkrement wird gewählt, z.B. 6, und bleibt konstant.
- Darüber hinaus muss ein Modul für die Uhrenmathematik gewählt werden, z.B. 5, und auch dieses bleibt konstant.
Nun haben wir alle notwendigen Parameter für unseren linearen Kongruenzgenerator zusammen. Jetzt können wir Schritt für Schritt losrechnen:
- Es geht mit der Multiplikation des Startwerts und des Faktors los, also 4 mal 3 gleich 12.
- Anschließend addiert man das Inkrement, also 12 plus 6 gleich 18.
- Dann berechnet man den Rest der Division des Ergebnisses mit dem Modul, also 18 mod 5. Das ist gleich 3.
Die 3 ist die erste generierte Zufallszahl. Sie wird zur Berechnung des nächsten Werts anstelle des Startwerts eingesetzt. Damit folgt als nächste Rechnung (3 mal 3 plus 6) mod 5 mit dem Ergebnis 0. Nun wird die 0, unsere nächste Zufallszahl, anstelle des Startwerts verwendet. Auf diese Weise geht es immer weiter.
Es gilt damit als Rechenvorschrift für den Kongruenzgenerator [ ( (Start-)Wert mal Faktor ) plus Inkrement ] mod Modul für den jeweils nächsten Zufallswert. Die entsprechende mathematische Notation ist
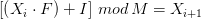
wobei 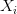 die Zufallszahlen (das i im Index zeigt nur an, die wievielte Zufallszahl gemeint ist),
die Zufallszahlen (das i im Index zeigt nur an, die wievielte Zufallszahl gemeint ist), 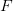 der Faktor,
der Faktor, 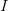 das Inkrement und
das Inkrement und 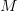 das Modul ist. Die Berechnung von Pseudozufallszahlen mit einem linearen Kongruenzgenerator geht auf den US-amerikanischen Mathematiker Derrick Henry Lehmer (1905-1991) zurück [1].
das Modul ist. Die Berechnung von Pseudozufallszahlen mit einem linearen Kongruenzgenerator geht auf den US-amerikanischen Mathematiker Derrick Henry Lehmer (1905-1991) zurück [1].
Schnell eintretende Langeweile
Führt man das obige Beispiel fort erhält man die Zufallszahlenreihe 4, 3, 0, 1, 4, 3, 0, 1, ... Dieses Ergebnis ist für einen Zufallsgenerator sehr unbefriedigend. Das liegt im Wesentlichen an zwei Dingen: Zum einen ist durch das sehr kleine Modul von 5 die Anzahl möglicher Zufallszahlen sehr stark begrenzt. Damit wiederholen sich die Zahlen sehr schnell. Durch ein hinreichend groß gewähltes Modul ergibt sich eine deutlich höhere Anzahl an möglichen Zufallszahlen. Zum anderen ist das Beispiel so schlecht konstruiert, dass nicht einmal alle Werte im Bereich des Moduls, also bis 5 durchlaufen werden. Es fehlt nämlich die 2. Man sagt auch, dass nicht die maximale Periodenlänge erreicht wird. Um einen linearen Kongruenzgenerator besser zu konstruieren gibt es einen Satz von Regeln [2], wie die verschiedenen Parameter gewählt werden müssen. Damit wäre eine maximale Periodenlänge gewährleistet. Jedoch hat der linearer Kongruenzgenerator nur einen begrenzten Nutzen. Die durch ihn generierten Pseudozufallszahlen sind aufgrund ihrer Vorhersagbarkeit für kryptografische Anwendungen nicht sicher, also nicht zufällig genug. Für einfache und unkritische Anwendungen ist er aber häufig ausreichend, so dass er in vielen Programmbibliotheken implementiert ist wie z.B. bei Java [3].
Lesen Sie hierzu auch...
Referenzen
[1] Donald Knuth, 1969: The Art of Computer Programming 2. Seminumerical Algorithms. Addison-Wesley Longman, Amsterdam.
[2] T. E. Hull, A. R. Dobell, 1962: Random Number Generators. SIAM Review, Vol. 4, No. 3, S. 230-254.
[3] Oracle, 2014: Java™ Platform, Standard Edition 7 API Specification. URL: http://docs.oracle.com/javase/7/docs/api/java/util/Random.html (29.01.2014)
Microlearning
