In einem der letzten Blog-Artikel haben wir das Pareto-Prinzip betrachtet. Dieser nach Vilfredo Pareto benannte Zusammenhang, auch als 80/20-Regel bekannt, bezeichnete einen Zustand der Ungleichverteilung, bei dem viele kleine Werte, im Gegensatz zu wenigen großen Werten, nur einen geringen Anteil einer Gesamtsumme ausmachen. Nun wollen wir uns die nach dem Ökonomen und Statistiker Max O. Lorenz (1880-1962) benannte Kurve ansehen, die eine grafische Darstellung von Ungleichverteilungen ist.
Von Vilfredo Pareto zu Max Lorenz
Die Pareto-Verteilung zeigte uns im Falle einer Ungleichverteilung von Einkommen, dass umfangreiche Einkommen zwar einen großen Beitrag zum gesamten Einkommen leisten. Allerdings kamen diese Einkommen nur sehr selten vor. Ablesen konnte man dies an den sehr geringen Werten auf der senkrechten Achse, die sehr großen Werten auf der horizontalen Achse zuzuordnen waren. Die so gezeigte Pareto-Verteilung ist daher eine Wahrscheinlichkeitsverteilung. Max Lorenz ging nun einen anderen Weg und zeigte mit seiner Abbildung, wie hoch der Anteil am Einkommen ist, der auf einen bestimmten Teil der Bevölkerung entfällt [1]. Diese Darstellung verdeutlicht damit gut die bereits genannte 80/20-Regel bzw. das Pareto-Prinzip.
Konstruktion der Lorenz-Kurve
Abb. 1: Koordinatensystem zur Darstellung der Lorenz-Kurve
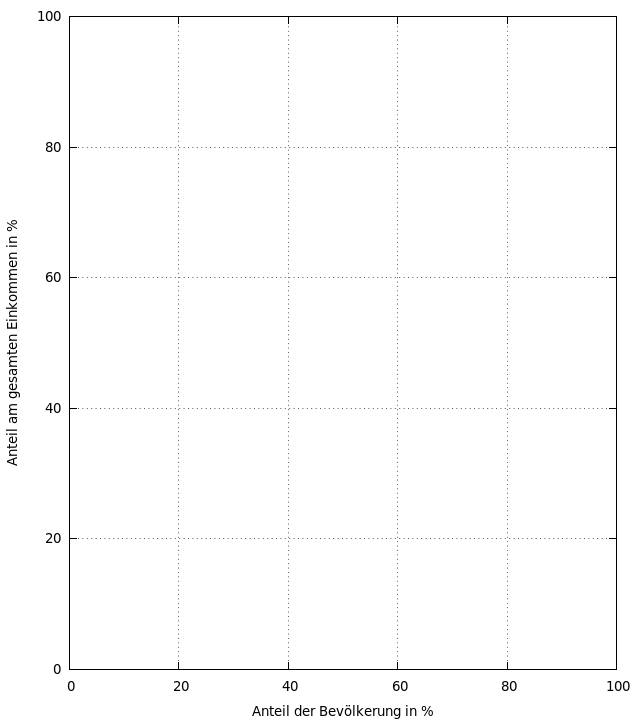
Um die Lorenz-Kurve zu zeichnen benötigen wir ein Koordinatensystem mit zwei Achsen. Auf der horizontalen Achse (genannt Abszisse) tragen wir die den Anteil der Bevölkerung auf. Die senkrechte Achse (Ordinate) weist dann entsprechend den dazugehörigen Anteil des Einkommens aus. Ein solches Koordinatensystem ist in Abbildung 1 zu sehen.
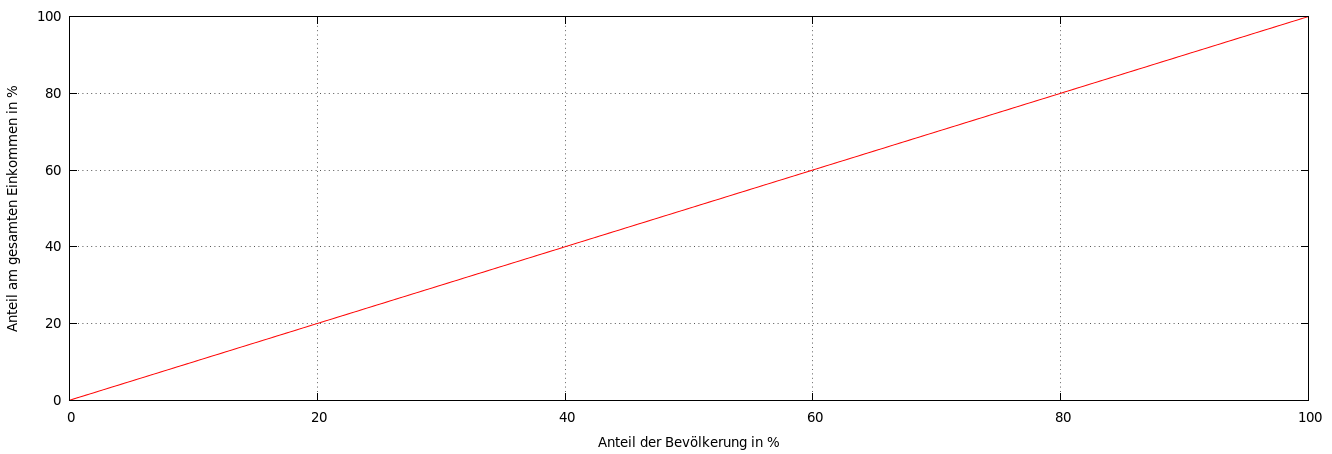
Nehmen wir nun in einem ersten Schritt an, die Einkommen in der Bevölkerung seien absolut gleich verteilt. Jeder Bürger hätte somit exakt das gleiche Einkommen wie alle anderen auch. Das würde bedeuten, dass 10% der Bevölkerung auch 10% des Einkommens verdienen. Ebenso würden die Relationen 50/50, 75/75 und auch 96,38/96,38 sowie alle anderen gleichwertigen Zuordnungen gelten. In diesem Fall wäre die Lorenz-Kurve eine gerade Linie. Abbildung 2 zeigt diesen Fall. Mit zunehmendem Anteil der Bevölkerung steigt auch gleichmäßig der Anteil des Einkommens. Es wird also immer die Bevölkerung und das Einkommen bis zum betrachteten Wert aufsummiert. Dieses Zusammenrechnen bis zu einer bestimmten Grenze - hier der beobachtete Wert - nennt man Kumulation.
Abb. 2.: Lorenz-Kurve mit Gleichverteilung
Lorenzkurve mit Bauch
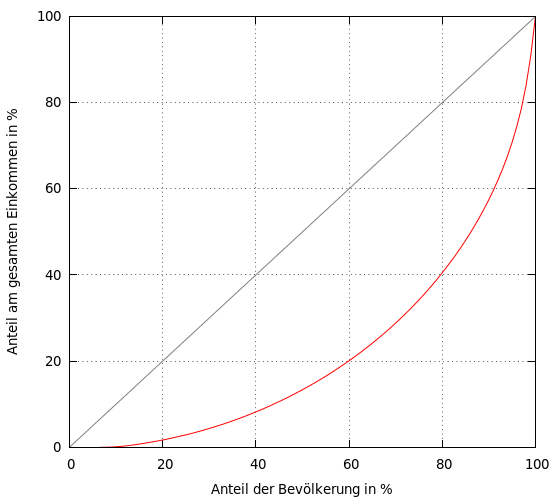
Wie bereits Vilfredo Pareto erkannt hatte, sind Einkommen fast nie gleichverteilt. Es gibt also einen kleinen Teil der Bevölkerung, der verhältnismäßig viel Einkommen erhält, während große Teile der Bevölkerung geringere Einkommen verdienen. Um eine Lorenz-Kurve zu konstruieren, die diese Ungleichverteilung wiedergibt, müssen wir zunächst die Einkommen nach ihrer Größe sortieren. Unsere Liste wird also mit dem Bezieher des geringsten Einkommens beginnen und mit der Person enden, die das Höchsteinkommen erhält.
Abb. 3: Lorenz-Kurve (rot) einer Ungleichverteilung (Gleichverteilung in grau)
Würden wir diese Sortierung nicht vornehmen, erhielten wir viele Sprünge im Graph entsprechend der sehr unterschiedlichen Abfolge von Einkommen. Dies liegt an der kumulierten Darstellung, die nur durch die Sortierung einen gleichmäßigen Verlauf ergibt. Nun werden die Werte aufsummiert nacheinander in das Koordinatensystem eingetragen. Da zu Beginn sehr geringe Einkommen eingetragen werden, die ebenso einen nur geringen Anteil am Gesamteinkommen ausmachen, wird der Graph anfangs nur sehr langsam ansteigen. Gegen Ende wird diese Steigung immer größer. Dies entspricht dann den hohen Einkommen, die einen großen Anteil am Gesamteinkommen bilden. Dadurch erhält die Lorenz-Kurve eine Art Bauch. Die Größe dieses Bauches entspricht dem Grad der Ungleichheit: Je größer der Bauch umso größer die Einkommensungleichverteilung. Der Bauch wird maximal bei einer maximalen Ungleichverteilung. Dann verläuft der Graph entlang der waagerechten Achse bis er beim letzten Wert sprunghaft auf 100% ansteigt. Dies ist dann die Person, die das gesamte Einkommen der Bevölkerung verdient.
Quantitative Messung
Die Auftragung der Lorenz-Kurve ist jedoch als Grafik nur eine qualitative Messung der Ungleichheit. Selbstverständlich wäre es möglich mehrere Lorenz-Kurven zum Beispiel von verschiedenen Nationen übereinander zu legen. Die Nation mit dem größten Bauch würde dann die größte Einkommensungleichverteilung aufweisen. Allerdings kann es passieren, dass sich Kurven schneiden. Dann ist aus der Grafik nicht mehr direkt eine vergleichende Aussage ableitbar.
An dieser Stelle setzt der Gini-Koeffizient an, mit dem wir uns im nächsten Teil der Reihe zur Ungleichheit (siehe unten) beschäftigen wollen. Er erlaubt es, die Ungleichheit durch die Berechnung eines Werts zu messen und baut dabei direkt auf der Lorenz-Kurve auf. Damit sind verschiedene Ungleichverteilungen direkt und einfach miteinander zu vergleichen.
Lesen Sie hierzu auch/demnächst...
Der Theil-Index (demnächst)
Referenzen
[1] Bundeszentrale für politische Bildung, 2013: Das Lexikon der Wirtschaft, Lorenzkurve. URL: http://www.bpb.de/nachschlagen/lexika/lexikon-der-wirtschaft/20031/lorenzkurve (03.03.2014)