Die Frage nach der Natur von Information ist nicht einfach zu beantworten. Das liegt unter anderem daran, dass dieser Begriff in vielen verschiedenen Bereichen verwendet wird. Als politischer Begriff, in der Kommunikationstechnik, durch Naturwissenschaft und sogar in Wirtschaftsbereichen wird Information auf unterschiedliche Weise verstanden und interpretiert. Ein wesentliches Element in Naturwissenschaft und Technik ist die Messung von Information [1]. Hierbei wird nicht von Information als einer Bedeutung gesprochen sondern die durch Claude E. Shannon (1916-2001) eingeführte statistische Sichtweise angewendet.
Der Weihnachtsabend
Stellen Sie sich vor, Sie packen an Weihnachten die Geschenke Ihrer Lieben aus. Insgesamt haben Sie zehn Präsente und machen sich voller Vorfreude ans Werk. In der ersten Schachtel finden Sie ein Paar Socken. Sie setzen ein Lächeln auf und denken sich nichts weiter dabei. Das zweite Paket hält wieder ein Paket Socken für Sie bereit, genauso wie das dritte und vierte. So langsam verschwindet Ihre Weihnachtsfreude und Sie sind etwas gereizt. Ein Wutausbruch unter dem festlich geschmückten Baum droht, als Sie feststellen, dass auch die Päckchen Nr. 5 bis 9 je ein Paar Socken enthalten. Sie denken sich: "Wenn das letzte Paket nun auch noch Socken enthält - und was soll es auch sonst enthalten - wird das gleich ein Weihnachten, was hier niemand mehr vergisst."
Sie öffnen langsam die letzte Schachtel und erblicken... das neue Smartphone, das Sie sich so sehnlich gewünscht haben! Es soll an dieser Stelle keine Erörterung über die Kommerzialisierung des Weihnachtsfests folgen, obwohl dieses Thema sicherlich auch passen würde. Vielmehr soll die Frage beantwortet werden, warum die Überraschung über das Smartphone mit den Socken viel größer ist, als wenn Sie nur das Smartphone bekommen hätten. Dieses Geschenk besitzt nämlich nicht nur einen deutlich größen materiellen Wert als neun Sockenpaare. Es hat darüber hinaus auch einen deutlich höheren Informationsgehalt.
Messung der Überraschung
In dem weihnachtlichen Beispiel wird durch das Auspacken der einzelnen Geschenkpakete die Unsicherheit Stück für Stück verringert. Zu Beginn ist es noch völlig unklar, was sich in den zehn Paketen verbirgt. Der Informationsgehalt, der insbesondere in dieser Situation auch Überraschungswert genannt werden kann, ist nun eng mit der Wahrscheinlichkeit für das Erscheinen eines Sockenpaars bzw. eines Smartphones in der Geschenkbox verknüpft.
Üblicherweise bezeichnet man Wahrscheinlichkeiten in der Wissenschaft mit dem Buchstaben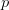 
. Da es insgesamt zehn Pakete gibt, von denen eins mit einem Smartphone und neun mit Strumpfwaren bestückt sind, ist die Wahrscheinlichkeit für ein Mobiltelefon
oder auch 10% und für ein Paar Socken
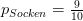
oder analog eben 90%. Über die Definition für den Informationsgehalt - den wir mit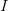 
bezeichnen wollen - sind wir nun in der Lage, den Informationsgehalt eines Paars Socken und den des Smartphones an diesem Weihnachtsabend zu berechnen. Sie lautet:
Diese Formel besagt, dass sich der Informationsgehalt über den negativen Logarithmus der Auftretenswahrscheinlichkeit berechnet (Der Logarithmus ist die Umkehrung des Potenzierens). Logarithmen werden immer zu einer bestimmten Basis gebildet, die hier mit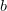 
gekennzeichnet ist. Für die Berechnung des Informationsgehalts muss an dieser Stelle die Anzahl aller möglichen Ereignisse eingesetzt werden. An diesem Weihnachtsabend sind entweder Socken oder das Smartphone möglich. Damit ist 
.
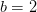Wie überraschend sind denn nun Socken und Telefon? Dazu setzen wir die oben genannten Wahrscheinlichkeiten in die Formel für den Informationsgehalt ein und bemühen einen Taschenrechner.
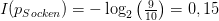
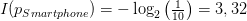
Der Informationsgehalt/Überraschungswert des Smartphones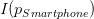 
ist über 20-mal so hoch wie der der Sockenpaare. Die berechneten Werte sind im Übrigen nicht von der Reihenfolge der Geschenke abhängig.
Geschenkempfehlung
Wir haben gesehen, dass sich der Informationsgehalt eines Zeichens über die Wahrscheinlichkeit des Auftretens berechnen lassen kann. Diese Größe ist ein wesentliches Element der durch Claude E. Shannon geprägten Informationstheorie, die nicht nur bei Kommunikationskanälen eine Rolle spielt, sondern auch in der Analyse komplexer Systeme zur Anwendung kommt.
Sie persönlich können aber darüber hinaus für das nächste Weihnachtsfest mitnehmen, dass es Sinn macht, vor dem zu verschenkenden Smartphone neun Sockenpaare als Präsent zu übergeben.
Referenzen
[1] C. E. Shannon, W. Weaver, 1994: The Mathematical Theory of Information. University of Illinois Press.