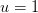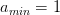Attraktor

Nicht nur im Wahlkampf und bei Stammtischdebatten wird leidenschaftlich über die Verteilung von Einkommen, Vermögen und Belastungen diskutiert. Die Messung solcher Disparitäten ist auch Gegenstand der Wirtschafts- und Sozialforschung. Durch die Bestimmung von Ungleichheitsmaßen verschiedener Länder werden beispielsweise deren Einkommenverteilungen - oder besser -ungleichverteilungen - in Relation gesetzt, um damit Rückschlüsse auf die jeweiligen Abstände zwischen Arm und Reich zu ziehen. Welche Messgrößen werden dabei herangezogen und was bedeuten die Ergebnisse? In einem ersten Schritt wollen wir dazu das Pareto-Prinzip betrachten.

Pareto-Prinzip: Viel Aufwand für wenig Ertrag - und umgekehrt

Wie viele Aufgaben erledigen Sie im Allgemeinen in einem Großteil der Ihnen zur Verfügung stehenden Zeit? Vielleicht denken Sie spontan, dass Sie 10% Ihrer Aufgaben in 10% der verfügbaren Zeit erledigt haben. Dies mag nicht gänzlich unmöglich sein, wäre allerdings ein sehr untypischer Fall. Ist es nicht vielmehr so, dass sie für viele kleine Aufgaben relativ wenig Zeit benötigen und für sehr umfangreiche einzelne Aufgaben viel Zeit? Es ist daher nicht eher so, dass Sie vielleicht etwa 60-80% Ihrer täglichen Aufgaben und Arbeiten in etwa 20-40% Ihrer Zeit erledigen. Oder umgekehrt benötigen Sie zum Beispiel für 10% Ihrer Verpflichtungen 90% Ihrer Zeit, weil diese Verpflichtungen so umfangreich und schwierig sind. Lassen Sie uns weiter fragen: Mit wie vielen Freunden und Bekannten verbringen Sie wie viel Zeit? Auch diese Frage dürfte auf ein ähnliches Ergebnis hinauslaufen. Sie haben wahrscheinlich ein paar wenige sehr gute Freunde und eine ganze Reihe von losen Bekannten. Sie treffen vielleicht in 90% Ihrer Freizeit immer die gleichen 10-20% Ihrer Freunde und Bekannten. Hingegen sehen Sie den Großteil Ihres sozialen Umfelds nur an eventuell 5% der verfügbaren Zeit.

Es ließen sich noch viele weitere Beispiele für das oben angedeutete Phänomen finden, das als 80/20-Regel oder Pareto-Prinzip bezeichnet wird. Vilfredo Pareto (1848-1923) entdeckte dieses Verhältnis Ende des 19. Jahrhunderts, als er Vermögens- und Einkommensverteilungen der Bevölkerung untersuchte [1]. Allgemein gesprochen bedeutet es, dass sich die Summe eines Gesamtwerts zum Großteil aus wenigen sehr hohen Werten zusammensetzt. Sehr viele geringe Werte machen dann nur einen kleinen Teil des Gesamtwertes aus.

Pareto-Verteilung

Die durch Pareto beschriebene Verteilung ist durch eine mathematische Vorschrift (sog. Wahrscheinlichkeitsdichte) definiert. Wir wollen uns diese anschauen, um zu verstehen warum diese Formel eine derartige Verteilung ergibt und wie wir daraus eine typische Regel nach dem Pareto-Prinzip ablesen können. Die Funktion lautet [2]

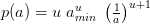
In dieser Formel finden Sie die Parameter und 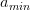, die wir der Einfachheit halber zunächst beide auf 1 setzen können und uns erst später mit einer Erklärung beschäftigen. Dadurch wird der gesamte Ausdruck für ungeübte Augen übersichtlicher:

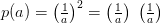
Bleiben wir, um die Formel zu verstehen und ohne Anspruch auf Exaktheit der Zahlen, bei unserem Beispiel von Aufgaben und wie viel Zeit Sie für diese Verpflichtungen benötigen. In der Formel ist dann der Umfang oder Aufwand einer Aufgabe das , wobei große Werte von einem großem Aufwand entsprechen. Wie viele Aufgaben Sie von dem jeweiligen Typ zu erledigen haben, können Sie auf der linken Seite der Gleichung mit dem 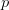berechnen. Das in Klammern hinter dem 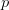auf der linken Seite brauch Sie nicht zu verunsichern. Es drückt nur aus, dass die Häufigkeit einer bestimmten Aufgabe von ihrem Aufwand abhängt - oder umgekehrt: Ohne zu wissen wie umfangreich eine Verpflichtung ist, könnten Sie auch nicht sagen wie oft Sie eine derartige Aufgabe erledigen müssen. Sie wissen ja gar nicht, welche Aufgabe genau gemeint ist.

Für verschiedene Werte von können Sie nun die dazugehörigen 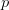ausrechnen:

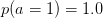
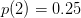
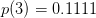
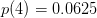
usw.

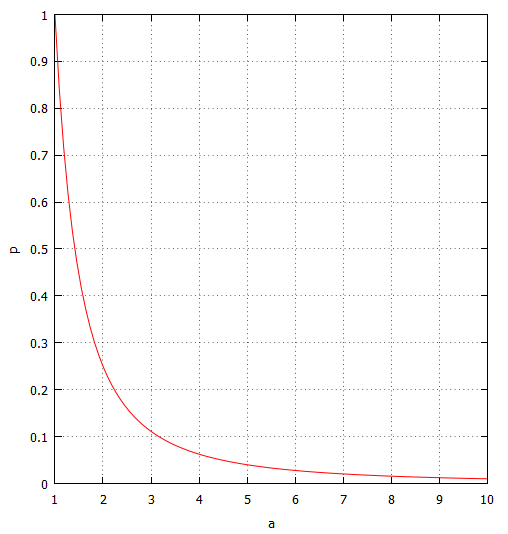
Würden Sie für alle nur möglichen Werte von zwischen 1 und 10 die entsprechenden 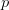ausrechnen und in ein Diagramm einzeichnen, sähe das Ergebnis wie in der nebenstehenden Abbildung 1 aus. Erinnern wir uns: Große Werte von bedeuten große, umfangreiche Aufgaben. Als Beispiel schauen wir auf 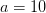. Wir können dann an der Kurve den korrespondierenden Wert für 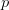ablesen. Er liegt bei 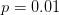. Diese relativ kleine Zahl bedeutet nichts anderes als dass solch aufwendige Verpflichtungen nur sehr selten vorkommen. Schauen wir uns auch das andere Ende der Kurve an. Hier lesen wir bei 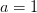einen Wert von 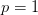und damit einen verhältnismäßig hohen Wert ab. Also kommen kleine, schnell erledigte Aufgaben (kleines )  sehr häufig vor (großes 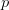). Zusammenfassend können wir festhalten, dass große Aufgaben nur selten, also in kleiner Anzahl vorkommen, jedoch sehr zeitraubend sind. Auf der anderen Seite gibt es viele kleine Aufgaben, die dadurch sehr häufig zu erledigen sind. Diese sind zusammengenommen jedoch in einem relativ kleinen Anteil der Zeit abgeschlossen. Damit gilt, wie bereits im ersten Abschnitt erwähnt: Die Summe des Gesamtwerts setzt sich größtenteils aus wenigen sehr hohen Werten und sehr viele geringe Werte zusammen.

Die Leistung von Vilfredo Pareto lag nun darin zu erkennen, dass diese Verteilung proportional zur von ihm untersuchten Einkommensverteilung war. Das bedeutet, dass die oben gezeigte Kurve und die Einkommensverteilung sich im gleichen Verhältnis ändern. Also kommen sehr große Einkommen selten vor, während es viele kleine Einkommen gibt. Der Schritt zur Messung der Ungleichheit besteht nun in der Interpretation der Parameter in der Formel, die wir bisher auf 1 gesetzt hatten.

Messung der Ungleichheit

Der Parameter 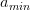gibt die linke Grenze der Verteilung an. An dieser Stelle ist der Wert von 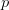maximal. Damit beeinflusst  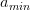lediglich die Lage oder Position der Kurve im Vergleich zur waagerechten Achse.

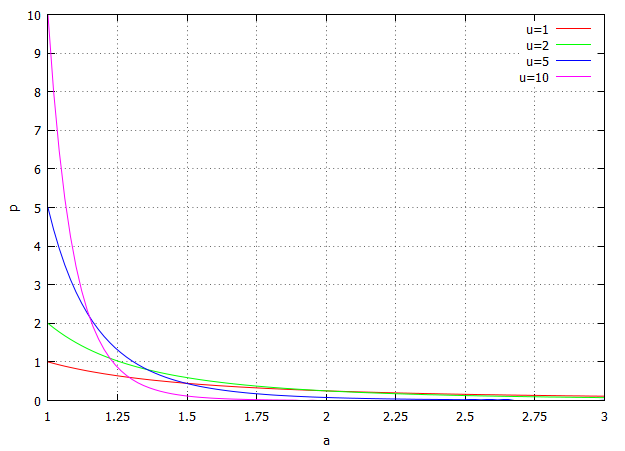
Er hat jedoch keinen Einfluss auf den genauen Kurvenverlauf, also die Krümmung des Graphs. Hierfür ist vielmehr der Parameter verantwortlich. Er ist damit die Kennziffer, die das Maß der Ungleichheit der Verteilung angibt [3]. Um dies zu verdeutlichen schauen wir uns verschiedene Verläufe der Funktion für unterschiedle an. In der Abbildung 2 sind exemplarisch vier verschiedene Kurvenverläufe dargestellt. Es ist zu erkennen, dass für ansteigende die Häufigkeit kleiner Werte zunimmt. Die pinke Kurve, die mit 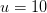errechnet wurde, liegt bei 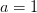deutlich über allen anderen Graphen und weist damit eine entsprechend größere Anzahl kleiner Werte aus.

Überträgt man dies auf die Einkommensverteilung bedeuten hohe Werte des "Ungleichheitsparameters" ein hohes Maß an Einkommensungleichheit. Sollte es also möglich sein, die Einkommensverteilungen verschiedener Staaten zu ermitteln und diese einer Pareto-Verteilung folgen, so ließe sich über die Bestimmung der jeweiligen Werte von eine Rangfolge der Einkommensungleichheit in diesen Staaten aufstellen. Diese Bestimmung von kann über eine mathematisches Verfahren recht einfach realisiert werden. In der Praxis wird nicht der Wert von für diesen Vergleich herangezogen, obgleich das Grundverständnis hierfür auch bei den angewandten Verfahren wichtig ist. Dazu können Sie in den hier demnächst erscheinenden oder bereits erschienenen Artikeln (siehe unten) mehr erfahren.

Sollten Sie in Zukunft Teilnehmer einer leidenschaftlich geführten Stammtischdebatte zum Thema Gerechtigkeit bzw. Ungleichheit sein, so bringen Sie doch einfach mal etwas mehr Mathematik ins Spiel. Fragen Sie Ihr echauffiertes Gegenüber doch danach, bei welchen Parametern der Pareto-Verteilung er nicht mehr das Gefühl hätte benachteiligt zu sein. Mal sehen, was er antwortet.

Lesen Sie hierzu auch/demnächst...

Die Lorenz-Kurve

Der Gini-Koeffizient

Der Theil-Index (demnächst)

Referenzen

[1] Vilfredo Pareto, 1897: Cours d'économie politique, Tome II

[2] Michael P. McLaughlin, 2013: A Compendium of Common Probability Distributions. Second Edition, v2.7, S. 61 f. URL: http://www.causascientia.org/math_stat/Dists/Compendium.pdf (27.01.2014)

[3] Benoît Mandelbrot, 1960: The Pareto-Lévy Law and the Distribution of Income. International Economic Review, 1, S. 79-106. URL: http://sage.math.washington.edu/home/wstein/www/home/simuw/simuw08/refs/fractal/mandelbrot-the_pareto_levy_law_and_the_distribution_of_income.pdf (28.01.2014)